La nascita della meccanica quantistica, parte 6: “Sullo spettro dell’idrogeno dal punto di vista della nuova meccanica quantistica”

(Indice delle puntate precedenti: parte 0, parte 1, parte 2, parte 3, parte 4, parte 5)

Wolfgang Ernst Friedrich Pauli nasce a Vienna il 25 Aprile 1900. Suo padre è un noto medico viennese che un anno prima della sua nascita, seguendo un suggerimento del suo ex professore Ernst Mach, decide di abbandonare la professione per dedicarsi completamente alla ricerca in chimica fisica (diventerà poi professore all’Università). Forse per sdebitarsi, visto l’ottimo consiglio ricevuto, dà a suo figlio il secondo nome Ernst e addirittura chiama Mach a fare da padrino per il suo battesimo, il che se non altro pone sin da subito sotto buoni auspici le sorti scientifiche del nuovo nato.

Le promesse vengono mantenute già a cominciare dal ginnasio, in cui durante le ore di lezione più noiose il giovane Wolfgang inganna il tempo leggendo sottobanco non delle riviste porno (come tutti gli adolescenti che si rispettino), ma… gli articoli di Einstein sulla relatività generale. L’argomento lo interessa così tanto che comincia a prendere lezioni private da tale Hans Bauer, professore all’università di Vienna e autore (assieme a un certo Erwin Schrödinger, di cui — come potete ben immaginare — riparleremo) di alcuni lavori sulla nuova teoria. Queste lezioni evidentemente danno i loro frutti se già nel settembre del 1918, appena tre mesi dopo aver ottenuto il diploma, Pauli è in grado di spedire a una rivista il suo primo articolo scientifico, che riguarda il calcolo del tensore energia-impulso del campo gravitazionale.

Dopo aver evitato l’arruolamento nell’esercito del morente impero austro-ungarico grazie a una presunta “debolezza di cuore” (Herzschwäche), Pauli decide di abbandonare Vienna e proseguire i suoi studi di fisica in Germania, all’università di Monaco. Non passa molto tempo prima che il suo talento venga riconosciuto da Sommerfeld che nel 1920, dopo aver dovuto incassare il rifiuto di Einstein, chiede proprio al nuovo arrivato di scrivere un articolo di review sulla relatività per un importante progetto editoriale dell’epoca chiamato Enciclopedia delle Scienze Matematiche, di cui è il coordinatore. Il prestigio di questo incarico si può misurare dal fatto che esso pone il ventenne Pauli sullo stesso piano di nomi quali Boltzmann, Lorentz, Debye, Born e lo stesso Sommerfeld, tutti autori di altri articoli per il medesimo progetto. Il lavoro, che alla fine ammonta a 237 pagine, è sostanzialmente completo per il dicembre di quell’anno ed esce a stampa nel settembre del 1921; successivamente pubblicato in monografico, su di esso si formeranno generazioni e generazioni di relativisti fino agli anni ’70 e oltre.

Alla fine del 1920, come sappiamo, anche Heisenberg si iscrive all’università di Monaco. I due legano immediatamente, nonostante sotto molti punti di vista siano uno l’opposto dell’altro: ad esempio mentre Heisenberg ama la montagna, lo sci e le escursioni, Pauli disdegna ogni tipo di attività fisica e non si allontana mai dalla città. Il suo passatempo preferito consiste nel trascorrere le serate nei caffé di Schwabing, celebre quartiere notturno di Monaco, per la gioia di Sommerfeld che la mattina non vede mai arrivare il suo studente prima di mezzogiorno.

È sempre in questo periodo che Pauli inizia a sviluppare quel terribile e irriverente senso critico per cui diventerà famoso (o famigerato) nella comunità internazionale dei fisici. Nel suo secondo articolo (che risale al giugno del 1919), dovendo segnalare un errore di segno in alcune formule di un lavoro di Hermann Weyl, Pauli scrive cautamente:

Vorrei esprimere, con il dovuto rispetto, l’opinione che un piccolo errore sia presente nell’articolo di Weyl.

Sfortunatamente, questa frase rimarrà l’unica critica gentile della sua carriera: già nella sua review sulla relatività Pauli non si fa alcun problema a sottolineare in maniera spietata alcune incongruenze fisiche nelle teorie di mostri sacri quali lo stesso Weyl e Gustav Mie. Questi e altri episodi gli varranno più avanti il nomignolo di “frusta di Dio” (die Geissel Gottes) affibbiatogli da Ehrenfest (e accettato con grande orgoglio). La sola persona che in qualche misura si salverà dai suoi commenti abrasivi sarà Sommerfeld, verso il quale manterrà per tutta la vita quel rispetto tipico del rapporto allievo-maestro. L’unica eccezione ce la racconta Heisenberg: un giorno, durante una lezione a cui Sommerfeld si è presentato vestito in maniera particolarmente pomposa, Pauli si gira verso l’amico e osserva: «non ti sembra che somigli a un vecchio colonnello ussaro?».

Nella seconda parte del suo periodo di studi a Monaco gli interessi di Pauli si spostano decisamente sulla fisica atomica, che in quel momento è ricca di problemi aperti (contrariamente alla relatività). È quindi del tutto naturale che la sua tesi di dottorato, discussa il 25 luglio del 1921, verta proprio sulla teoria dei quanti, e precisamente sul problema di descrivere lo ione della molecola di idrogeno. Il lavoro è tecnicamente impressionante, ma i risultati sono una delusione: l’energia di ionizzazione calcolata tramite il modello di Bohr-Sommerfeld non coincide con il valore misurato, a dimostrazione del fatto che la “corretta” meccanica quantistica è ancora lontana.

Ottenuto il titolo di dottore, Pauli va a Göttingen per un semestre come assistente di Max Born, che entusiasta scrive in una lettera all’amico Einstein: «non avrò mai più un assistente così bravo». Questo giudizio si rivelerà un po’ troppo affrettato: come Born ricorderà in seguito, «gli piaceva dormire fino a tardi, e più di una volta gli capitò di perdere la lezione delle undici. A un certo punto abbiamo iniziato a mandare la nostra cameriera da lui alle dieci e mezza per accertarsi che fosse sveglio. Senza dubbio era un genio di prim’ordine, ma la mia preoccupazione era ingiustificata. Il suo successore Heisenberg era altrettanto intelligente, e molto più coscienzioso: non abbiamo mai dovuto mandare nessuno a svegliarlo».

Nell’aprile del 1922 Pauli, non gradendo l’atmosfera troppo matematica che si respira a Göttingen, si trasferisce ad Amburgo presso l’istituto di fisica diretto da Wilhelm Lenz; appena due mesi dopo, però, è nuovamente a Göttingen per il Bohr Festspiele (di cui abbiamo già parlato nella seconda puntata). Come Heisenberg, anche Pauli resta affascinato dalla figura di Niels Bohr, tanto che in seguito descriverà questo incontro come “l’inizio di una nuova fase della mia vita scientifica”. Bohr, dal canto suo, pensa bene di invitarlo per un anno a Copenhagen come curatore dell’edizione in tedesco dei suoi lavori. A questa straordinaria proposta Pauli risponde, con notevole faccia tosta:

Mi riesce difficile pensare che avrò qualche difficoltà sul piano scientifico, ma l’imparare una lingua straniera come il danese va di gran lunga oltre alle mie abilità.

al che Bohr non può fare a meno di scoppiare a ridere. Pochi mesi più tardi, nell’ottobre del 1922, Pauli arriva effettivamente alla corte di Bohr dove, oltre a portare avanti il già menzionato incarico editoriale, ha modo di avviare una fruttuosa collaborazione con Hendrik Kramers e si dedica altresì a ricerche personali su un altro dei grandi problemi aperti dell’epoca, l’effetto Zeeman anomalo, ottenendo però solo dei risultati parziali e certamente poco soddisfacenti per un fisico della sua ambizione. La frustrazione che tale problema causa al povero Pauli è testimoniata da un celebre aneddoto: un giorno un suo collega all’istituto di Bohr lo incontra mentre va a spasso per le vie di Copenhagen con il muso lungo. «Sembri molto triste», osserva questi ignaro. E Pauli, scocciato: «Come si può avere un’espressione felice mentre si pensa all’effetto Zeeman anomalo?».

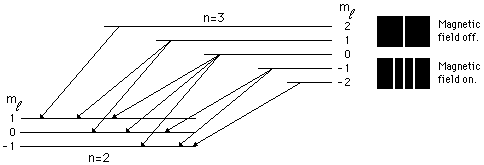
Tra parentesi, è forse il caso di spiegare brevemente cosa diavolo sia questo effetto Zeeman anomalo. Come ricordato nella prima puntata, ogni elemento chimico ha una sua “carta d’identità” data dalle sue righe spettrali, e uno dei problemi principali che doveva affrontare la nuova meccanica era proprio quello di spiegare la struttura di tali spettri. Nel 1896 Pieter Zeeman, un fisico olandese operante a Leiden, ha l’idea di provare a vedere cosa succede a queste righe spettrali quando la sostanza che le emette viene immersa in un campo magnetico statico. Ebbene, ciò che accade è che alcune righe spettrali si dividono: ad esempio per l’idrogeno, la riga che corrisponde alla trasizione da \(n=3\) a \(n=2\) diventa un tripletto (la figura che segue è spudoratamente copiata da qui):

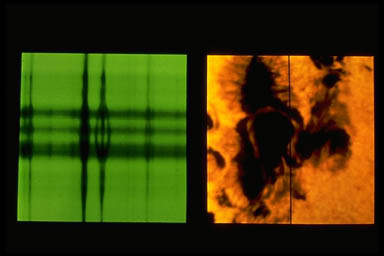
Siccome l’entità dello scostamento dipende dal valore del campo magnetico, questo effetto viene usato oggi ad esempio per misurare i campi magnetici delle macchie solari:

Per questa scoperta Zeeman vincerà il premio Nobel nel 1902 assieme a Lorentz, che fornisce una spiegazione teorica del fenomeno nell’ambito della meccanica classica.

Ma qual è la ragione dell’aggettivo “anomalo”? Il problema è che per certi elementi le righe spettrali si dividono in una maniera più complicata rispetto al semplice tripletto previsto dal modello di Lorentz (o dalla sua versione quantistica, sviluppata da Debye e Sommerfeld nel 1916). Ad esempio nel sodio abbiamo divisioni in 4 o addirittura in 6 righe distinte:

Oggi sappiamo che il numero di righe dipende dallo spin degli elettroni di valenza degli atomi coinvolti, ma all’epoca lo spin era sconosciuto e queste differenze di comportamento tra i vari elementi costituivano un vero rompicapo che tenne occupati molti tra i grossi calibri del periodo, tra cui ricordiamo anche Heisenberg e Alfred Landé.

(Per inciso, anche la scoperta dello spin dell’elettrone meriterebbe di essere raccontata, tanto più che lo stesso Pauli ha avuto in essa una parte tutt’altro che trascurabile; ma dato che questa puntata sta già diventando fin troppo lunga, mi sembra più opportuno lasciarla da parte per il futuro.)

Torniamo dunque a Pauli che nell’ottobre del 1923, esaurito il suo incarico a Copenhagen, ritorna ad Amburgo dove, su pressione dei colleghi Lenz e Otto Stern (appena trasferitosi da Francoforte, dove assieme a Walter Gerlach aveva ideato e condotto il celebre esperimento omonimo), viene rapidamente nominato Privatdozent senza neanche bisogno di una tesi di abilitazione (oggi diremmo per “chiara fama”). Ed è proprio ad Amburgo che, poco più di un anno più tardi, arriva la scoperta che proietta definitivamente Pauli nell’olimpo dei fisici teorici: il principio di esclusione.

Pauli passa buona parte del 1924 a cercare di spiegare la struttura elettronica degli atomi, prendendo come punto di partenza il cosiddetto «principio di costruzione» (Aufbauprinzip), discusso tra l’altro da Bohr durante le sue lezioni a Göttingen di due anni prima, secondo cui la struttura elettronica di ciascun elemento della tavola periodica può essere “costruita” a partire da quella dell’idrogeno aggiungendo un elettrone alla volta. La svolta arriva quando Pauli, leggendo la prefazione alla quarta edizione fresca di stampa dell’Atombau und Spektrallinien di Sommerfeld, trova il riferimento a un importante lavoro sulla struttura degli atomi (pubblicato il 1° ottobre 1924) a opera di Edmund Stoner, fisico sperimentale inglese di stanza al Cavendish Laboratory. In breve tempo, Pauli è in grado di ricondurre le regole empiriche dedotte da Stoner sulla base dei suoi esperimenti di spettroscopia a raggi X a un singolo principio: in un atomo non possono mai esistere due o più elettroni con gli stessi numeri quantici. Non solo: tale ipotesi permette anche di spiegare la lunghezza dei vari periodi della tavola periodica (la famosa sequenza 2, 8, 18, 32 che fino ad allora era stata vista come un puro dato empirico), alcune regolarità nella struttura degli spettri, e molto altro.

Questi importanti risultati vengono pubblicati nel marzo del 1925 in un articolo che diventa immediatamente un classico, tanto che per la fine dell’anno il «principio di esclusione di Pauli» sarà già entrato stabilmente a far parte delle leggi della fisica atomica (e frutterà a Pauli il premio Nobel, seppur a vent’anni di distanza). Pauli stesso, comunque, non resta pienamente soddisfatto del suo lavoro, soprattutto per non essere riuscito a giustificare il nuovo principio a partire da assunzioni teoriche di carattere più generale (cosa che avverrà successivamente tramite il legame con le proprietà di simmetria della funzione d’onda). In una lettera indirizzata a Bohr e Heisenberg scriverà al riguardo, nel suo classico stile sarcastico:

In questo lavoro non ci sono sciocchezze (Unsinn) peggiori delle attuali opinioni riguardo la struttura degli spettri. Piuttosto, le mie sciocchezze sono coniugate rispetto a quelle abituali fino ad oggi.

Archiviato il lavoro sul principio di esclusione, Pauli mette in cantiere un nuovo, monumentale progetto: viene infatti incaricato da Geiger (sì, quello del contatore) e Scheel, curatori dell’Handbuch der Physik, di scrivere (ancora!) un articolo di review, stavolta sulla teoria dei quanti. Il momento non poteva essere scelto peggio (anche se ovviamente all’epoca né Pauli né chiunque altro poteva prevederlo), visto che nei mesi successivi la teoria di Bohr-Sommerfeld sarebbe stata completamente spazzata via dalla “nuova” meccanica quantistica; tant’è vero che quando la review in questione (un altro tomo di 278 pagine) vedrà effettivamente la luce, nel luglio del 1926, sarà già irreparabilmente obsoleta, e Pauli si riferirà ad essa ironicamente come il suo «vecchio testamento».

L’articolo per l’Handbuch tiene impegnato Pauli fino alla metà di ottobre; nel frattempo, in quel di Göttingen, la meccanica delle matrici è in piena costruzione e Pauli è costantemente aggiornato sui suoi sviluppi grazie alle lettere di Heisenberg. Il 9 ottobre scrive a Kronig:

La meccanica di Heisenberg mi ha ridato gioia di vivere (Lebensfreude) e speranza. Non dà la soluzione del mistero, ma adesso credo di nuovo che sia possibile fare dei progressi.

Poche righe dopo, però, fa capire chiaramente come non sia molto felice della direzione che la nuova teoria sta prendendo sotto l’influsso di Born e Jordan:

Prima di tutto bisognerebbe provare a liberare la meccanica di Heisenberg dal diluvio di erudizione formale di Göttingen, e metterne a nudo l’essenza fisica in maniera migliore.

Tale insoddisfazione viene probabilmente espressa allo stesso Heisenberg, che in una lettera di pochi giorni dopo (12 ottobre) gli risponde piccato:

Il tuo eterno vituperare Copenhagen e Göttingen è un vero scandalo. In ogni caso, devi concederci che non stiamo cercando di rovinare la fisica di proposito. Quando ci rimproveri dicendo che siamo talmente asini che non abbiamo mai prodotto niente di nuovo dal punto di vista fisico, puoi anche avere ragione. Ma allora anche tu sei ugualmente asino, visto che neanche tu ci sei riuscito.

Pauli accetta la sfida implicita nelle parole dell’amico e, nel giro di tre settimane, riesce laddove Born e Heisenberg avevano fino a quel momento fallito, ovvero nel ricavare la corretta espressione dei livelli energetici dell’atomo di idrogeno usando la nuova meccanica. Per farlo usa quello che potremmo definire un “asso nella manica”: il vettore di Laplace-Runge-Lenz, una particolare costante del moto tipica del problema dei due corpi interagenti tramite un potenziale di tipo coulombiano. (Apparentemente questo vettore, pur essendo per ovvi motivi ben noto ad Amburgo — no, quel Lenz a capo del dipartimento non è un omonimo — non lo era altrettanto nella pur “erudita” Göttingen.)

Ovviamente la prima persona ad essere informata del successo è Heisenberg, che il 3 novembre risponde soddisfatto:

Non c’è bisogno che io ti dica quanto sono felice per la tua nuova teoria dell’idrogeno, e quanto ammiri il fatto che tu l’abbia messa a punto così velocemente…

Ma Pauli non si ferma qui: è anche in grado di calcolare la perturbazione ai livelli energetici indotta dalla simultanea presenza di (deboli) campi elettrici e magnetici, problema questo che dava origine a gravi difficoltà nell’ambito della vecchia teoria dei quanti. L’articolo che contiene questi risultati, intitolato “Sullo spettro dell’idrogeno dal punto di vista della nuova meccanica quantistica”, viene ricevuto dallo Zeitschrift für Physik il 17 gennaio 1926 ma, a causa di alcune lungaggini editoriali, sarà effettivamente pubblicato solamente più di due mesi dopo, il 27 marzo.

In quello stesso periodo, come sappiamo, il problema dell’atomo di idrogeno viene attaccato anche in Inghilterra da Dirac, che però lo affronta in una maniera molto più generale, di fatto risolvendo il problema della quantizzazione di un qualunque sistema espresso in termini di variabili azione-angolo. Applicando tale teoria al caso dell’atomo di idrogeno, Dirac è in grado di calcolare i relativi livelli energetici arrivando a un’espressione del tipo

\(\omega_{n} = \frac{m e^{4}}{2\hbar} \left( \frac{1}{P^2} – \frac{1}{(P+n\hbar)^{2}}\right)\)

Sulla base di ragionamenti euristici assume poi che la quantità che ha chiamato \(P\) sia pari a un multiplo intero di \(\hbar\), il che gli permette di ricondurre la formula precedente a quella ottenuta da Bohr. Questi risultati andranno a costituire il suo lavoro successivo, “La meccanica quantistica e uno studio preliminare dell’atomo di idrogeno“, completato il 22 gennaio del 1926 (cinque giorni dopo quello di Pauli). Nel frattempo, Dirac ha già saputo da Heisenberg della soluzione dell’atomo di idrogeno nella meccanica delle matrici a opera di Pauli, e ha anche ricevuto le bozze del relativo articolo (che infatti citerà in una nota a pié di pagina). Tuttavia sarà la soluzione di Dirac ad andare in stampa per prima, nel fascicolo di marzo dei Proceedings della Royal Society, grazie al suo canale preferenziale con la rivista in questione. Ciò nonostante, la priorità nel trattamento dell’atomo di idrogeno sulla base della nuova meccanica verrà in genere riconosciuta a Pauli, sulla base delle date di ricezione degli articoli da parte delle rispettive riviste (i cinque giorni sopra ricordati). Per la seconda volta, il povero Dirac si vedeva superato in volata sul traguardo; e a poco valeva, come consolazione, la solita lettera di Heisenberg che si congratulava per i risultati ottenuti.

L’anno 1926 si apre quindi all’insegna dell’ottimismo: finalmente la fisica atomica non sembra più quel mistero inestricabile che era apparsa per vent’anni. La nuova meccanica, sia essa considerata nella sua versione matriciale made in Göttingen o in quella più algebrica propugnata con tenacia da Dirac, ha già dimostrato di essere all’altezza della vecchia teoria dei quanti di Bohr e promette di andare ben oltre. Tutto ci si poteva aspettare a questo punto, tranne che all’orizzonte si affacciasse una terza teoria, dal carattere completamente diverso rispetto alle due appena ricordate e in aperta competizione con esse! Eppure, sarà proprio quello che succederà; ma per capire come dobbiamo nuovamente fare un salto indietro nel tempo di poco più di un anno, per raccontare di quando un giovane nobile francese mise in grande imbarazzo quattro celebri professori della Sorbona… (continua)