Come sapete, da un po’ di tempo a questa parte ho eletto il Lisp, e più precisamente il suo dialetto Scheme, a mio linguaggio di programmazione preferito (in attesa di trovare il tempo di imparare lo Haskell). Una delle cose che più mi piace di Scheme è la sua grande concisione rispetto a linguaggi di programmazione “tradizionali” come il C e i suoi derivati. Basti pensare alla quantità di codice che è necessario scrivere per implementare una funzione polimorfa in Scheme (dove è essenzialmente banale) e, ad esempio, in C++ usando i template e tutto il resto. Personalmente, trovo che la concisione sia una qualità molto importante: più la sintassi di un linguaggio è semplice, più i programmi scritti in quel linguaggio rispecchiano la struttura dell’algoritmo astratto che essi realizzano. Viceversa un linguaggio troppo verboso tende a nascondere le idee fondamentali in un sottofondo di codice inutile. Non bisogna però cadere nell’eccesso opposto, ovvero nella tentazione di rendere un linguaggio “il più conciso possibile”, il che può compromettere un’altra qualità molto importante: la facilità di lettura del codice.
Queste riflessioni sono ispirate da un vecchio articolo in cui mi sono imbattuto recentemente che riguarda il linguaggio di programmazione J, ideato negli anni ’90 da Ken Iverson come successore della sua precedente creazione APL. Si tratta di un linguaggio molto diverso da quelli mainstream, sotto molti punti di vista. In particolare, la sua peculiare sintassi permette di scrivere programmi molto più concisi rispetto al loro equivalente in un linguaggio convenzionale. Ma la domanda è: ne vale la pena? Prendiamo ad esempio il codice illustrato nell’articolo di cui sopra:
+/1e6<,!/~>:i.100
Anche se a prima vista è difficile crederlo, questa stringa di 17 caratteri è un programma completo in J; esso calcola il numero di coefficienti binomiali \(n\choose k\) maggiori di un milione, per \(n\) e \(k\) che variano da 1 a 100. Rimando all’articolo sopra citato per una spiegazione dell’algoritmo utilizzato.
La cosa interessante è che la stessa identica strategia risolutiva (sostituendo gli array con le liste) può essere implementata in Scheme, perdendo un po’ in concisione ma guadagnando enormemente in trasparenza del codice. Proviamo a fare questo esercizio di traduzione, seguendo l’algoritmo così come spiegato dal buon Tardieu.
Anzitutto dobbiamo generare una lista dei primi 100 numeri naturali. Non casualmente, nella libreria srfi-1 c’è una funzione iota che è l’esatta traduzione dell’operatore i di J (e di APL). Quindi la nostra prima mossa sarà
(iota 100)
Proprio come in J, questo genera in realtà la lista dei numeri da 0 a 99, quindi occorre incrementare ciascun numero di una unità:
(map 1+ (iota 100))
Qui ho usato la procedura 1+ predefinita del mit-scheme, ma in qualunque altro interprete Scheme basterebbe usare la procedura anonima (lambda (x) (+ x 1)).
Supponiamo di avere già a disposizione una procedura (binom n k) che calcola il coefficiente binomiale di \(n\) e \(k\); dobbiamo costruire una tabella formata dai risultati di questa procedura per \(n\) e \(k\) che assumono ciascuno dei valori contenuti nella lista creata precedentemente. La soluzione di questo problema si ottiene, come ben sa chiunque abbia letto il secondo capitolo di SICP, annidando due applicazioni di map. Il fatto che dobbiamo utilizzare lo stesso argomento per due volte significa che il problema ci sta supplicando di introdurre una procedura apposita, e noi lo accontentiamo:
(define (table f x)
(map (lambda (n)
(map (lambda (k)
(f n k))
x))
x))
Questa procedura ritorna una lista di liste (la versione Lispiana di una matrice), ma noi vogliamo dimenticarci della suddivisione in righe e ottenere semplicemente una lista con tutti i coefficienti binomiali che abbiamo calcolato; vogliamo cioè “schiacciare” la nostra lista di liste, il che si fa usando reduce con append:
(reduce append
'()
(table binom (map 1+ (iota 100))))))
Dunque questo codice genera una lista con tutti i coefficienti binomiali desiderati. Per concludere occorre sostituire ciascuno di questi numeri con 1 o con 0 a seconda che esso sia maggiore di un milione o meno:
(map (lambda (n) (if (> n 1000000) 1 0))
(reduce append
'()
(table binom (map 1+ (iota 100))))))
e infine sommare tutti i risultati, ancora con reduce:
(reduce +
0
(map (lambda (n) (if (> n 1000000) 1 0))
(reduce append
'()
(table binom (map 1+ (iota 100))))))
(In realtà, da un punto di vista Lispiano sarebbe probabilmente più naturale usare filter per eliminare dalla lista tutti i numeri minori di un milione e ritornare come risultato la lunghezza della lista risultante; ma qui stiamo semplicemente facendo un esercizio di traduzione letterale, e quindi ci dobbiamo attenere all’algoritmo originario che è pensato per operare su array di lunghezza fissa piuttosto che su liste di lunghezza variabile.)
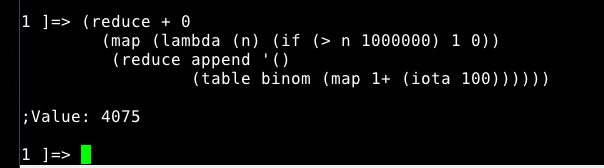
La prova del fuoco:
che è il risultato corretto.
Il bello è che i due programmi, l’originale in J e la sua traduzione in Scheme, si possono praticamente mettere in corrispondenza biunivoca:
Mi sembra inutile evidenziare quale delle due versioni sia maggiormente leggibile. Forse non è un caso se J e APL sono stati definiti, ironicamente ma fino a un certo punto, linguaggi di sola scrittura.