 Werner Heisenberg nasce a Wurzburg (ridente cittadina tedesca oggi probabilmente più nota per aver dato i natali a Dirk Nowitzki) il 5 Dicembre 1901, ma quando ha appena 8 anni si trasferisce con tutta la famiglia a Monaco di Baviera, dove il padre è stato nominato professore di greco all’università.
Werner Heisenberg nasce a Wurzburg (ridente cittadina tedesca oggi probabilmente più nota per aver dato i natali a Dirk Nowitzki) il 5 Dicembre 1901, ma quando ha appena 8 anni si trasferisce con tutta la famiglia a Monaco di Baviera, dove il padre è stato nominato professore di greco all’università.
Nel 1914 frequenta il ginnasio a Monaco quando scoppia la prima guerra mondiale: l’edificio viene occupato dall’esercito e la normale vita scolastica viene sconvolta. Heisenberg ne approfitta per studiare per conto suo (e forse con risultati migliori) le materie che più lo interessano, ovvero fisica e matematica; in quest’ultima riesce particolarmente bene, tanto che a 15 anni fa da tutore (oggi diremmo che dà ripetizioni) di analisi a un amico di famiglia che frequenta il primo anno di università.
Quanto fosse difficile essere adolescenti in Germania durante quegli anni si può intuire da un paio di aneddoti. Con il protrarsi della guerra e l’aumentare delle vittime il numero di soldati abili nell’esercito cala drammaticamente, e così un bel giorno il giovane Heisenberg e tutti i suoi compagni di classe vengono arruolati all’interno di un’organizzazione paramilitare e sottoposti a un vero e proprio addestramento in vista del futuro impiego al fronte. Fortunatamente nel 1918 la guerra finisce, ma la situazione in Germania è comunque instabile per via delle insurrezioni comuniste ispirate dalla rivoluzione di Ottobre in Russia. Il gruppo paramilitare entra quindi ugualmente in azione, non sul fronte francese ma per le strade di Monaco. Heisenberg scriverà in seguito riguardo a quell’esperienza:
Ero un ragazzo di 17 anni e la presi come una sorta di avventura. Era come giocare a guardie e ladri…
Il secondo aneddoto riguarda l’estate del 1918, in cui Heisenberg viene inserito in un’altra associazione «volontaria» e spedito in una fattoria dell’hinterland bavarese a lavorare i campi rimasti incolti per la carenza di manodopera; compito reso ancora più duro dal razionamento del cibo dovuto alla guerra. Heisenberg passa il (poco) tempo lasciatogli libero dalla zappa giocando a scacchi con i suoi sventurati compagni, leggendo qualche libro di matematica che aveva portato con sé e tentando vanamente di dimostrare l’ultimo teorema di Fermat.
Per fortuna la situazione piano piano si normalizza, il ginnasio riapre i battenti e nel 1920 Heisenberg può finalmente sostenere l’Abitur (l’analogo del nostro esame di maturità), che gli apre la strada per l’università. L’idea, peraltro facile da intuire visti i trascorsi, è quella di diventare un matematico e in particolare di occuparsi di teoria dei numeri. Non è probabilmente un caso che a Monaco insegni sin dal 1893 Ferdinand von Lindemann, vera e propria autorità in materia il cui nome, tra l’altro, è ricordato ancora oggi per essere stato il primo a dimostrare (nel 1882) che \(\pi\) è un numero trascendente.
Così, nell’ottobre del 1920, Heisenberg si reca da Lindemann per chiedergli di fungere da supervisore per i suoi studi universitari. Le premesse erano ottime visto che Lindemann, nel corso della sua lunga carriera, aveva seguito più di sessanta studenti di dottorato tra cui nientemeno che David Hilbert, semplicemente il più grande matematico dell’epoca (che incontreremo nelle puntate finali del nostro viaggio). Ma qui il destino ci mette per la prima volta lo zampino: Lindemann, che è a due anni dalla pensione e probabilmente non ha più voglia di impegnarsi in progetti di ricerca a lungo termine, decide di rifiutare l’offerta del giovane studente e gli suggerisce invece di rivolgersi a un suo ex allievo che, guarda caso, in quel momento dirige il dipartimento di fisica della medesima università… tale Arnold Sommerfeld, su cui a questo punto è il caso di spendere due parole.
Nel 1920 Sommerfeld ha 52 anni ed è ormai universalmente riconosciuto come uno dei padri fondatori della «teoria dei quanti». A sua volta un matematico di formazione, viene poi persuaso ad occuparsi di fisica per merito di Felix Klein, del quale era stato assistente a Gottingen alla fine del secolo precedente, e finisce per fondare dal nulla (come già ricordato) l’istituto di fisica a Monaco, nel quale dirige in prima persona anche gli esperimenti. Soprattutto, è un ottimo supervisore: come racconta l’amico Max Born,
…ha la rara abilità di trovare sempre del tempo da dedicare ai suoi studenti, nonostante i suoi doveri di insegnamento e di ricerca… Nella sua maniera amichevole e informale di insegnare, un ruolo importante avevano gli inviti a sciare al Sudelfeld, a due ore di treno da Monaco. Qui possedeva assieme al suo meccanico un rifugio. Alla sera, dopo una cena semplice, si lavavano i piatti, si discuteva del tempo e della neve e alla fine il discorso virava invariabilmente sulla fisica matematica; e per i suoi studenti più ricettivi si trattava di un’occasione d’oro per venire a conoscenza dei pensieri che giravano in testa al loro maestro.
Nel primo semestre di studi Heisenberg, forse non ancora del tutto convinto della scelta fatta, segue sia dei corsi di matematica che dei corsi di fisica; ma già all’inizio del secondo semestre decide di dedicarsi completamente a quest’ultima, tanto da superare anche lo scoglio dei corsi sperimentali obbligatori. Ben presto fa la conoscenza di un altro allievo di Sommerfeld, più vecchio di lui di poco più di un anno, e che tuttavia è già una sorta di celebrità nell’ambiente della fisica teorica tedesca; il suo nome è Wolfgang Pauli, e avremo modo di riparlare a lungo di lui in una delle prossime puntate. Comincia così un sodalizio che accomunerà i due, sia sul piano personale che su quello scientifico, per tutta la vita.
Nel frattempo passano i semestri e si avvicina il momento di iniziare l’attività di ricerca. Heisenberg è attratto dalla recentissima teoria della relatività, ma Pauli, che proprio in quel periodo sta scrivendo quello che diventerà il primo libro sulla nuova teoria, con notevole intuito gli suggerisce di lasciare perdere la relatività, in cui le previsioni vanno d’accordo con le osservazioni, e di dedicarsi invece alla fisica atomica, dove teoria ed esperimenti non collimano. Il primo articolo di Heisenberg (datato 17 dicembre 1921) riguarda quindi l’effetto Zeeman anomalo.
Nel giugno del 1922 Niels Bohr viene invitato a Gottingen per tenere un ciclo di lezioni sulla struttura degli atomi che verrà ribattezzato in modo semi-scherzoso il «Bohr Festspiele» (festival di Bohr). Si tratta di un vero e proprio evento, a cui partecipano un centinaio di fisici da tutta la Germania (e non solo: ad esempio Ehrenfest arriva da Leiden). Ovviamente è invitato anche Sommerfeld che decide di portare con sé Heisenberg, nonostante questi sia appena al suo quarto semestre di università. La visita si rivelerà decisiva sotto diversi punti di vista. Tanto per cominciare, Heisenberg è affascinato dall’ambiente di Gottingen, dove la teoria dei quanti è oggetto di intensa ricerca sia dal lato teorico (Born) che da quello sperimentale (Franck e collaboratori). Ma soprattutto, è impressionato da Bohr: dalle sue idee sulla struttura dell’atomo e ancor di più dal suo modo di fare fisica, molto diverso da quello del suo maestro Sommerfeld. Usando le categorie di oggi, potremmo dire che mentre il secondo era il prototipo del fisico matematico, il primo era invece un classico esponente della genia dei fisici teorici, per i quali le intuizioni contano molto di più delle dimostrazioni. Nelle parole di Heisenberg:
…dal modo in cui parlava della struttura atomica, ci si rendeva facilmente conto che da un punto di vista matematico non aveva dimostrato nulla; semplicemente, lui sapeva che le cose stavano più o meno così. […] Prendeva i suoi argomenti estremamente sul serio, e allo stesso tempo si rendeva conto di non poterli davvero dimostrare.
L’occasione per i due di fare conoscenza arriva in un modo un po’ particolare ma, credo, abbastanza tipico dei rapporti umani tra scienziati (di qualunque epoca). Durante la terza lezione, Bohr espone alcuni risultati del suo allievo e collaboratore Hendrik Kramers sull’effetto Stark quadratico. Heisenberg conosce bene quei risultati e non è convinto della loro correttezza, così al termine della lezione affronta Bohr e gli espone le sue perplessità. Lì per lì Bohr dà una risposta evasiva, ma si capisce che anche lui ha intuito la serietà dell’obiezione. Terminate le discussioni Bohr, evidentemente impressionato dalla perspicacia del giovane studente, ritorna da Heisenberg e lo invita a una passeggiata con lui nei boschi della vicina collina dell’Hainberg. La passeggiata in questione durerà ben tre ore, durante le quali i due, oltre a godere della splendida vista su Gottingen,
avranno modo di discutere in dettaglio su i numerosi problemi aperti della fisica atomica. Heisenberg scopre così che persino il fondatore della teoria dei quanti è profondamente preoccupato dalle difficoltà che essa incontra nello spiegare i dati sperimentali. Un messaggio importante che Heisenberg porta a casa da questo colloquio è che la conoscenza della natura deve sempre partire dai fenomeni, e solo in un momento successivo può essere fissata in uno schema formale; o, come ama dire Bohr, ciascuna situazione sperimentale deve essere descritta tramite concetti che si adattino ad essa.
Nel semestre invernale 1922/23 Sommerfeld parte per gli Stati Uniti, non prima di aver lasciato al suo allievo un problema di idrodinamica classica a cui lavorare per la tesi. Heisenberg, dopo aver ottenuto alcuni risultati preliminari su questo argomento, è impaziente di tornare a occuparsi di fisica atomica e si trasferisce armi e bagagli a Gottingen per lavorare con Born. I due si dedicano a una delle più spinose questioni irrisolte del momento: la descrizione quantistica degli atomi con più di un elettrone, e in special modo dell’elio, che pur sembrando non troppo più complicato dell’idrogeno si era fino a quel momento dimostrato refrattario a qualunque tentativo. Born ha però una nuova idea per attaccare il problema: mettere in campo la teoria delle perturbazioni, con la quale era familiare grazie a lavori precedenti sulla dinamica dei solidi cristallini. Sfortunatamente, anche questo nuovo approccio non riesce a riprodurre lo spettro dell’elio in maniera corretta; si fa così strada nei due l’idea che per compiere ulteriori progressi sia necessario alterare in maniera radicale qualcuno dei presupposti alla base del modello di Bohr-Sommerfeld. In un articolo del 1924 Born propone addirittura un nome per questa nuova (e ancora sconosciuta) teoria: Quantenmechanik.
Intanto, nell’estate del 1923, Heisenberg ritorna a Monaco, conclude la sua tesi di idrodinamica e supera (nonostante qualche difficoltà nella parte sperimentale) l’esame di dottorato. Dopo una vacanza di un mesetto in Finlandia lo ritroviamo nuovamente a Gottingen nell’ottobre del 1923, dove continua a lavorare con Born; questa volta l’oggetto di studio è lo spettro delle molecole complesse, dove i loro metodi danno risultati almeno qualitativamente corretti. Il 28 luglio 1924 riceve l’abilitazione che gli permette di insegnare nelle università tedesche. Subito dopo però si materializza, grazie a una borsa di studio Rockefeller, la possibilità di trascorrere nove mesi a Copenhagen da Bohr e Kramers, che Heisenberg coglie al volo. Durante questo soggiorno scrive con Kramers un articolo sulla diffusione della luce da parte degli atomi (5 gennaio 1925) che, come vedremo, giocherà un ruolo importante più avanti.
Siamo così arrivati, finalmente, alla fatidica primavera del ’25. Heisenberg è tornato a Gottingen, dove è Privatdozent, e nel frattempo cerca di ottenere sulla base della teoria dei quanti una formula che descriva l’intensità delle righe spettrali dell’idrogeno, ma senza successo. Guidato da quell’attitudine “rivoluzionaria” di cui abbiamo già parlato, decide allora di provare a modificare l’apparato concettuale della teoria di Bohr in un senso ancora più radicale, abbandonando ogni pretesa di descrizione dell’atomo in termini classici.
In particolare Heisenberg comincia a guardare con sospetto all’idea che nozioni quali posizione e velocità si possano applicare ai costituenti dell’atomo, per esempio agli elettroni. La ragione di ciò (almeno in questo momento, cioè nel maggio del 1925; successivamente le cose cambieranno) è non tanto e non solo l’impossibilità di una misura diretta di tali grandezze, visto che tale circostanza potrebbe essere puramente accidentale (il progresso della tecnica può infatti rendere possibili misure che in un certo momento storico appaiono impossibili). Piuttosto, un motivo ben più valido per rigettare i concetti classici è che, semplicemente, le teorie costruite basandosi su di essi non funzionano, cioè non riproducono i risultati sperimentali. In altre parole, Heisenberg qui mette in pratica il principio che Bohr stesso gli aveva insegnato tre anni prima durante quella passeggiata nei boschi attorno a Gottingen, secondo cui sono i concetti che devono adattarsi agli esperimenti e non viceversa.
Heisenberg decide così di cercare una descrizione dell’atomo in cui le quantità cinematiche classiche siano sostituite da grandezze che hanno un significato fisico diretto quali frequenza e intensità delle linee spettrali. Ma come procedere in concreto? Classicamente, la posizione di un punto materiale soggetto a un moto periodico si può esprimere tramite una serie di Fourier:
\(x(t) = \sum_{\alpha} x_{\alpha} e^{2\pi i \nu \alpha t}\)
Nella teoria dei quanti le ampiezze \(x_{\alpha}\) e la frequenza \(\nu\) dipendono anche da un numero naturale \(n\) («numero quantico»), e si ha quindi un’espressione del tipo
\(\sum_{\alpha} x_{n,\alpha} e^{2\pi i \nu_{n,\alpha} t}\)
e il principio di corrispondenza di Bohr afferma allora che un termine quale \(\nu_{n,n-\alpha}\) può essere interpretato come la frequenza della radiazione emessa in una transizione da \(n\) a \(n-\alpha\). L’idea di Heisenberg è quella di assumere che anche le ampiezze \(x_{n,n-\alpha}\) abbiano un significato analogo (legato stavolta all’intensità della radiazione emessa, che è data dal loro modulo quadro), e che l’insieme formato dalle quantità \(x_{n,n-\alpha}\) e \(\nu_{n,n-\alpha}\) possa giocare il ruolo che classicamente è ricoperto dalla posizione. (L’idea di considerare delle «ampiezze di transizione» tra livelli energetici come variabili dinamiche fondamentali era già presente nell’articolo di Born del 1924 citato in precedenza, a cui Heisenberg aveva collaborato.) A questo punto entra in gioco una nostra vecchia conoscenza, il principio di combinazione di Ritz, che in termini di frequenze si può scrivere come
\(\nu_{ik} = \nu_{ij} + \nu_{jk}\)
dove \(i,j,k\) è una qualunque terna di numeri quantici. Imponendo la validità di questa formula, Heisenberg arriva alla conclusione «quasi irrefutabile» secondo cui il prodotto di due insiemi di ampiezze di transizione \(x_{n,\alpha}\) e \(y_{n,\beta}\) si ottiene facendo uso della seguente “strana” regola:
\((xy)_{n,\alpha} = \sum_{\beta} x_{n,n-\beta} y_{n-\beta,n-\alpha}\)
In particolare il prodotto \(xy\) risulta essere, in generale, diverso dal prodotto \(yx\)! Heisenberg rimane molto perplesso da questa situazione, che non aveva mai incontrato fino a quel momento, ma non si lascia intimorire più di tanto e prova ad andare avanti. Ora, nella teoria di Bohr-Sommerfeld la soluzione di un problema dinamico si ottiene in due passi: il primo consiste nel risolvere l’equazione (classica) del moto, il secondo nell’applicare le condizioni di quantizzazione. Con l’aiuto del dizionario messo a punto in precedenza, per Heisenberg non è difficile trasformare un’equazione del moto in una relazione tra ampiezze di transizione; ma la traduzione delle condizioni di quantizzazione è ben altro problema, e nessuna soluzione ovvia è in vista. Così, all’inizio di giugno, Heisenberg ha la sensazione di trovarsi a un punto morto.
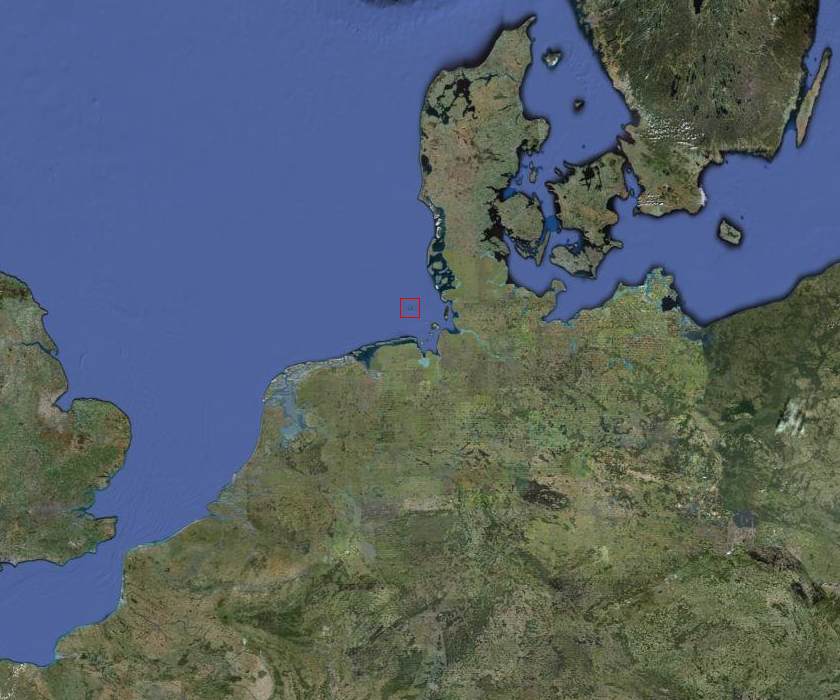
Ma qui c’è un nuovo colpo di fortuna: Heisenberg è allergico. Caso vuole che la primavera del ’25 in bassa Sassonia sia particolarmente ricca di pollini, e di conseguenza il povero Werner è tormentato da quello che allora si chiamava raffreddore da fieno (e oggi chiameremmo rinite allergica). Il medico gli consiglia così di cambiare aria e trasferirsi per dieci giorni in Heligoland, una minuscola isola nel mare del Nord la cui posizione nell’immagine satellitare qui sotto ho ritenuto opportuno evidenziare con un riquadro rosso:
Da questa visuale aerea si può intuire quanto numerose e diverse siano le attrattive e le distrazioni offerte dal luogo:
Heisenberg può così dedicarsi per qualche giorno esclusivamente a riflettere sulla sua nuova meccanica, e finisce per compiere due passi in avanti fondamentali. Anzitutto riesce finalmente a reinterpretare nel suo schema le condizioni di quantizzazione di Bohr-Sommerfeld, usando un trucco (la sostituzione di derivate con differenze) che aveva già impiegato nel suo articolo sulla diffusione della luce con Kramers. Scopre così che nel nuovo approccio le regole di quantizzazione diventano delle regole di somma, oltretutto equivalenti ad alcune relazioni già ottenute qualche mese prima da Kuhn e Thomas. Giunto a questo punto è finalmente in grado di applicare il formalismo a dei problemi concreti, e uno dei primi sistemi a cui si dedica è l’oscillatore armonico, per il quale ottiene quell’espressione dei livelli energetici
\(E = \frac{h\omega}{2\pi} (n + \frac{1}{2})\)
che oggi fa parte del bagaglio comune a ogni studente di fisica. Il risultato è significativo perché differisce dall’espressione prevista dalla vecchia teoria dei quanti, in cui manca l’addendo \(1/2\). Inoltre, dopo una notte di conti, riesce a dimostrare che l’energia del sistema risulta essere conservata nel tempo, il che è importante perché rappresenta una prima verifica della consistenza logica della nuova meccanica. E così, alle tre del mattino, terminati i calcoli ma troppo agitato per poter dormire,
…mi recai alla punta meridionale dell’isola, dove avevo da tempo voglia di scalare una roccia che sporgeva a picco sul mare. Nelle condizioni in cui mi trovavo fui in grado di farlo senza troppi problemi, e giunto in cima aspettai che sorgesse il sole…
Con la mente, e il naso, liberi il nostro eroe può così fare ritorno a Gottingen, non senza una fermata intermedia ad Amburgo, dove nel frattempo si era trasferito Pauli, per mettere al corrente l’amico dei nuovi sviluppi. Tornato finalmente a casa Heisenberg, ancora incerto sulla reale importanza del suo lavoro, prepara un articolo in cui espone per filo e per segno i risultati fin lì ottenuti e il 9 luglio lo spedisce a Pauli, pregandolo di fargli avere i suoi commenti in merito entro due o tre giorni. Il tempo stringe perché per la fine di luglio Heisenberg ha già accettato un invito a Cambridge per tenere una conferenza, e vuole a tutti i costi «finire l’articolo nei giorni che precedono la partenza, o gettare tutto nel fuoco».
Fortunatamente la risposta di Pauli non tarda ad arrivare ed è positiva (il che è già un fatto estremamente raro), così Heisenberg prende coraggio e il 12 luglio affida il manoscritto a Born (che fino a quel momento aveva tenuto all’oscuro di tutto) chiedendogli, nel caso lo ritenesse meritevole, di comunicarlo per la pubblicazione sullo Zeitschrift für Physik. (La peer-review a quell’epoca funzionava in una maniera un po’ diversa da quella di oggi…) Born, che in quel momento è esausto perché le lezioni del semestre estivo sono appena terminate, lì per lì posa il manoscritto sulla sua scrivania senza prestarvi troppa attenzione; ma qualche giorno dopo, quando finalmente gli dà un’occhiata, ne è letteralmente affascinato. La decisione se pubblicarlo o meno dev’essere stata facile se già il 15 luglio scrive, in una lettera all’amico Einstein,
Presto apparirà un nuovo articolo di Heisenberg; sembra molto mistico, ma è certamente corretto e profondo…
L’articolo,dal titolo Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen («Su una reinterpretazione quantistica delle relazioni cinematiche e meccaniche»), sarà ricevuto dalla rivista il 29 luglio e apparirà in stampa solo a dicembre di quell’anno; ma il suo contenuto si diffonderà molto più rapidamente, per mezzo di copie manoscritte (niente fotocopie a quei tempi!), lettere, seminari, etc., e metterà in moto una vera e propria rivoluzione a seguito della quale nulla, nella fisica atomica, sarà più come prima… (continua)


Alberto complimenti! Lettura appassionante!
Grazie! Ma il merito è della storia più che del narratore 🙂