La nascita della meccanica quantistica, parte 1: il contesto fisico

Dopo aver brevemente riepilogato lo stato del mondo nel 1925, occorre ora rendere conto dello stato in cui si trova la fisica. La situazione è per molti versi l’esatto opposto di quella che viviamo oggi: una marea di dati sperimentali, e nessuna teoria in grado di spiegarli! (Inutile sottolineare in quale delle due epoche un fisico, potendo scegliere, preferirebbe vivere…)

Il principale problema aperto è, naturalmente, quello di spiegare la struttura dell’atomo; i dati in proposito arrivano copiosi grazie al perfezionarsi di due diverse tecniche sperimentali di grande importanza. La prima è costituita dagli esperimenti di diffusione, o scattering, nei quali si studia in che modo fasci di particelle di vario tipo tra quelle allora note (alfa, beta, gamma) interagiscono con la materia. Ed è proprio dai risultati di un esperimento di diffusione con particelle alfa che Ernest Rutherford è in grado di dedurre, nel 1911, che la quasi totalità della massa di un atomo si trova concentrata in una regione di dimensioni relativamente piccole (dell’ordine di \(10^{-15}\) m per l’idrogeno) ed elettricamente carica, circondata da una carica uguale ed opposta distribuita all’interno di una sfera di raggio molto più grande (dell’ordine di \(10^{-10}\) m).

Emerge così il «modello planetario», secondo cui un atomo è composto da un nucleo centrale di carica \(Ze\) (dove \(Z\) è un numero intero, detto il numero atomico, mentre \(e\) è l’unità di carica elettrica, misurata per la prima volta da Millikan nel 1913) circondato da \(Z\) elettroni (scoperti da J. J. Thomson nel 1897) che “orbitano” attorno al nucleo come tanti pianeti attorno a una stella. Piccolo problema: secondo la meccanica classica, un sistema di questo tipo non è stabile! Gli elettroni, muovendosi all’interno del campo elettrico generato dal nucleo, dovrebbero infatti perdere progressivamente energia per irraggiamento fino a cadere sul nucleo. Questa difficoltà del modello fu chiara a tutti sin dal principio, ma si sperava che qualche fenomeno non ancora compreso potesse mettere a posto le cose.

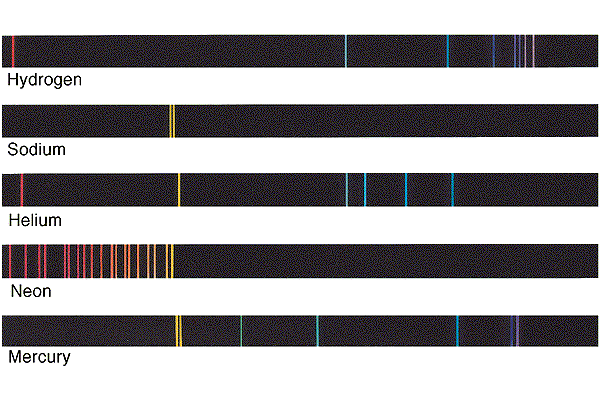
La seconda tecnica che permette di dare un’occhiata all’interno degli atomi è la spettroscopia, che nasce come scienza a metà ‘800 con la scoperta, a opera di Bunsen e Kirchhoff, che ciascun elemento chimico ha un suo spettro di emissione caratteristico formato da una sequenza discreta di righe aventi lunghezza d’onda ben definita, come quelli mostrati nella figura qui sotto (presa impunemente da qui):

Ben presto si comincia a sospettare che queste righe possano fornire degli indizi sulla struttura interna di atomi e molecole; viene così accumulata una mole impressionante di dati sugli spettri delle varie sostanze, che però si rivelano essere talmente complicati da eludere qualunque tentativo di trovarvi delle regolarità. Gli sforzi si concentrano allora sullo spettro dell’atomo più semplice in assoluto: l’idrogeno.

Il primo a gettare un po’ di luce su questo enigma non è però un fisico ma un curioso personaggio di nome Johann Balmer. Costui, dopo aver concluso gli studi con un dottorato in matematica (disciplina nella quale non risulta aver lasciato tracce significative), finisce per passare la sua vita professionale come insegnante in una scuola secondaria femminile di Basilea. Avvicinandosi ai 60 anni e non avendo evidentemente nulla di meglio da fare per passare il tempo, decide di dedicarsi all’analisi dei dati spettroscopici. Questa scelta dà i suoi frutti quando, nel 1885, annuncia al mondo con orgoglio che la lunghezza d’onda delle quattro righe spettrali dell’idrogeno allora note si può ottenere sostituendo i valori di \(n\) da 3 a 6 nella seguente espressione:

\(\lambda = L \frac{n^{2}}{n^{2} – 4}\)

dove \(L\) è una costante. Quasi subito vengono osservate altre righe spettrali di quella che oggi si chiama la serie di Balmer, e le relative lunghezze d’onda risultano in accordo con quelle prescritte dalla formula per \(n>6\).

Il passo successivo si deve allo svedese Johannes Rydberg che, essendo (contrariamente a Balmer) un fisico di professione, aveva imparato dal folklore degli spettroscopisti che il parametro giusto per classificare le righe spettrali non è tanto la lunghezza d’onda quanto il suo inverso, il numero d’onda \(k = \lambda^{-1}\), a sua volta legato alla frequenza dalla relazione \(\nu = ck\). In termini del numero d’onda la formula di Balmer si scrive

\(k = \frac{1}{L} \frac{n^{2}-4}{n^{2}} = \frac{4}{L} \left( \frac{1}{2^{2}} – \frac{1}{n^{2}}\right)\)

e tale espressione suggerisce immediatamente la forma più generale

\(k = R\left( \frac{1}{m^{2}} – \frac{1}{n^{2}}\right)\)

nota appunto come formula di Rydberg. Per \(m=2\) e \(n\geq 3\) si riottengono i numeri d’onda della serie di Balmer, ma la novità è che anche per altri valori di \(m\) questa formula descrive (al variare di \(n>m\)) delle sequenze di righe spettrali dell’idrogeno: per \(m=3\) si ha la serie di Paschen nell’infrarosso (osservata nel 1908), per \(m=1\) la serie di Lyman nell’ultravioletto (osservata nel 1914), e così via.

Un’ulteriore progresso si ha con il principio di combinazione di Ritz (1909), secondo cui non solo per l’idrogeno, ma anche per ogni altro atomo o molecola il numero d’onda di una riga spettrale può essere espresso come differenza tra due termini, detti per l’appunto termini spettrali. In tutta generalità si può dunque scrivere

\(k = T_{m} – T_{n}\)

Per l’atomo di idrogeno è ovviamente \(T_{n} = R/n^{2}\). La molteplicità delle righe negli spettri più complessi può così essere ridotta a un numero molto minore di dati, indicizzati (e questo, come vedremo, sarà un particolare molto importante) da coppie di numeri naturali.

Con il principio di Ritz il problema di descrivere empiricamente gli spettri si può ritenere risolto; occorre ora giustificare le formule così ottenute. Di nuovo, la meccanica classica si trova in gravissima difficoltà: essa richiede infatti che le frequenze caratteristiche di un moto periodico («armoniche») si possano sempre esprimere come una combinazione lineare a coefficienti interi di un certo numero di frequenze fondamentali. Nulla di tutto ciò si osserva negli spettri, in cui le frequenze, come si è visto, obbediscono invece al principio di combinazione di Ritz. Inizia così a farsi strada l’idea che per spiegare gli spettri sia necessario partire da idee completamente nuove, che presumibilmente coinvolgono l’ancora misterioso quanto d’azione di Planck.

Seguendo fino in fondo quest’intuizione, nel 1913 un ventottenne fisico danese il cui nome probabilmente non vi è ignoto, Niels Bohr, propone un modello dell’atomo di idrogeno che supera le difficoltà sopra ricordate, ma ad un prezzo molto caro: la definitiva rinuncia alla meccanica classica! Bohr parte dal già citato modello planetario dell’atomo, ma introduce due postulati completamente nuovi:

• un elettrone non può occupare un’orbita di raggio qualsiasi attorno al nucleo; esiste invece un insieme discreto di orbite permesse, o stazionarie;
• la radiazione viene emessa solo ed esclusivamente nel passaggio da un’orbita stazionaria all’altra, e la relazione tra frequenza ed energia emessa è quella data da Planck: \(\Delta E = h \nu\).

Ora, queste due ipotesi sono contraddittorie se assunte all’interno della fisica classica e siccome, come ben sanno i logici in ascolto, ex falso sequitur quodlibet (da principi contraddittori si può dedurre qualunque cosa) c’è voluto tutto l’istinto e il senso fisico di Bohr per cavarne fuori conclusioni sensate. Un ruolo fondamentale per stabilire le energie delle orbite permesse è giocato dal principio di corrispondenza (che però verrà chiamato in questo modo solo a partire dal 1920), secondo cui la frequenza della radiazione emessa in una transizione deve tendere, nel limite di orbite molto grandi, al valore previsto dalla meccanica classica. Grazie a quest’unica idea-guida Bohr fu in grado di derivare dal suo modello una formula per i termini spettrali dell’idrogeno, ottenendo così un’espressione della costante empirica di Rydberg in termini di altre costanti più fondamentali quali massa e carica dell’elettrone e, ovviamente, il quanto d’azione \(h\):

\(R = \frac{2\pi^{2} m e^{4}}{h^{3}}\)

che risulta in ottimo accordo con le misure spettroscopiche. Fu questa derivazione di \(R\) che, più di ogni altra cosa, convinse i contemporanei di Bohr della bontà del suo modello. Un’ulteriore conferma arriva nel 1914 con l’esperimento di Franck e Hertz (quest’ultimo nipote del più celebre scopritore delle onde elettromagnetiche), che rende evidente il carattere discreto dei livelli energetici negli atomi.

Negli anni successivi molti tra i maggiori fisici teorici dell’epoca si dedicano allo studio e allo sviluppo delle idee di Bohr; nasce così quella che in seguito, con l’affermarsi della MQ vera e propria, sarà chiamata la «vecchia teoria dei quanti». Basterà qui citare ad esempio un fondamentale lavoro di Einstein del 1917, in cui il fresco padre della relatività generale colma una lacuna che affligge il modello di Bohr chiarendo il meccanismo con cui gli atomi emettono e assorbono radiazione (se avete mai sentito parlare dei coefficienti di Einstein, sappiate che sono introdotti in questo articolo) e i lavori di Sommerfeld, Debye e altri che estendono i postulati di Bohr al caso di orbite ellittiche e ai sistemi (integrabili) con più gradi di libertà.

Nonostante questi promettenti sviluppi, comunque, la «teoria dei quanti» resta complessivamente in uno stato poco soddisfacente: ad esempio ogni tentativo di applicazione agli spettri degli atomi con più di un elettrone (a cominciare da quello dell’elio) fallisce miseramente. Un paio di citazioni renderanno bene l’idea della situazione: Jammer afferma

In spite of its high-sounding name and its successful solutions of numerous problems in atomic physics, quantum theory, and especially the quantum theory of polyelectronic systems, prior to 1925, was, from the methodological point of view, a lamentable hodgepodge of hypotheses, principles, theorems, and computational recipes rather than a logical consistent theory.

e van der Waerden rincara:

The research work during the years 1919-1925 that finally led to Quantum Mechanics may be described as systematic guessing, guided by the Principle of Correspondence.

Le capitali indiscusse della nuova teoria sono Copenhagen, dove Bohr chiede e ottiene nel 1921 l’apertura di un nuovo istituto di fisica teorica che oggi è giustamente a lui intitolato, e Göttingen, dove sono attivi Max Born (del quale riparleremo) e il già citato Franck. Subito dopo viene il dipartimento di fisica teorica dell’università di Monaco, dove opera Sommerfeld (è persino riduttivo definirlo il “capo”, considerato che l’intero dipartimento è stato creato a seguito della sua nomina a professore nel 1906), e quindi Berlino, dove però c’è la “vecchia guardia”: Planck (che nel 1925 ha 67 anni) e Einstein (che ne ha 46). Altri luoghi che giocheranno un ruolo importante sono Parigi, Zurigo e Cambridge, come vedremo. Il testo sacro su cui si formano i giovani studenti è il libro Atombau und Spektrallinien (“struttura atomica e linee spettrali”) di Sommerfeld, giunto alla sua quarta edizione.

Questa è dunque la situazione alla fine del 1925 quando, a seguito di una curiosa serie di circostanze, compare sullo Zeitschrift für Physik l’articolo di un giovane, e relativamente poco conosciuto, fisico tedesco che modificherà radicalmente lo scenario… (continua)